
First, about terminology:
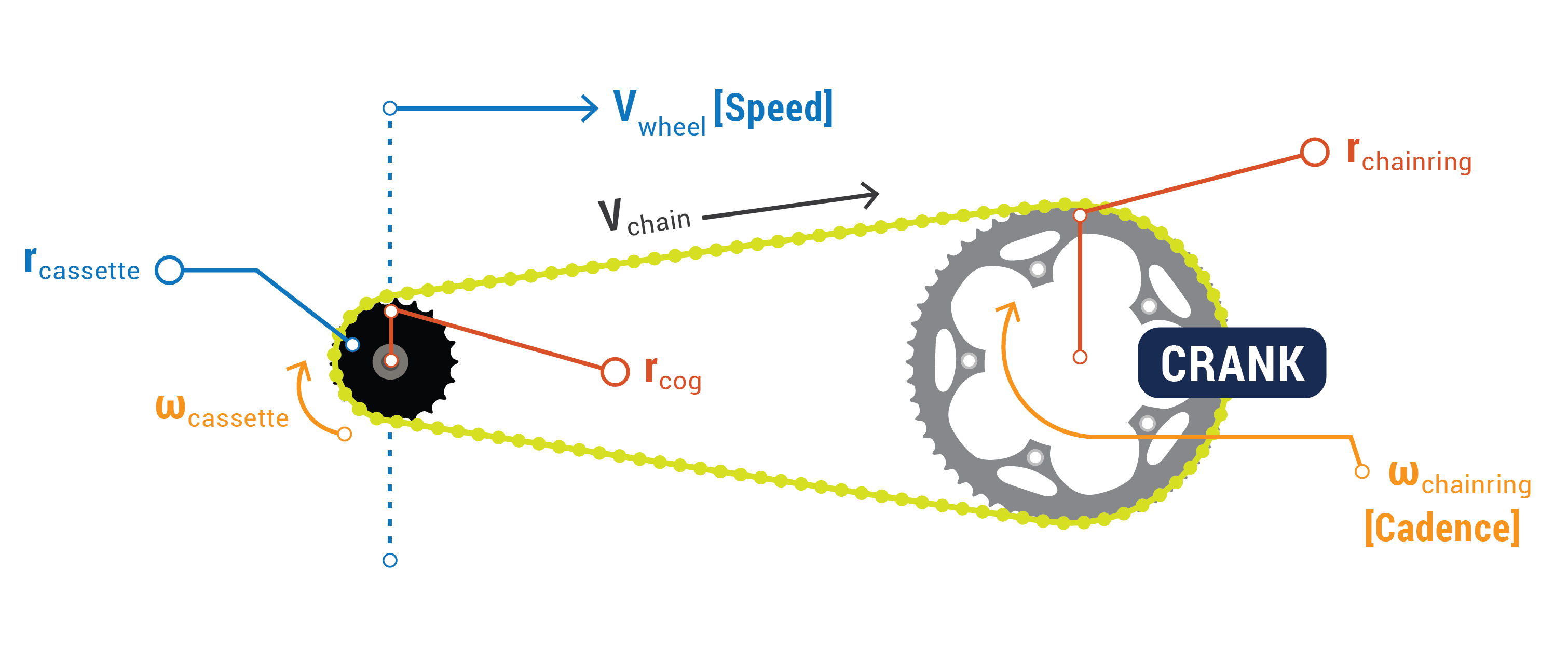
'Rear' set of cogwheels called 'cassette', it has 'cogs'. 'Frontal' set of cogwheels called chainring (on crankset/chainset), also 'cogs'. Chain between them is 'chain', it has 'links'.
Here is a random internet shop for bikers I googled in search of some real data.
This cassette has the following set of cogwheels with 12,14,16,18,21,26,32 cogs.
This chainring has 30, 39, 50 cogs.
There are two random chains on this internet shop, one with 116 links, another with 126 links.
Now I write a Python script to find GCD of each pair of cassette/chain and chainring/chain:
#!/usr/bin/env python3
import math
cassette=[12,14,16,18,21,26,32]
chain=[116,126]
chainring=[30,39,50]
print ("cassette, chain")
for x in cassette:
for y in chain:
print (f"{x} {y} {math.gcd(x,y)}")
print ("chainring, chain")
for x in chainring:
for y in chain:
print (f"{x} {y} {math.gcd(x,y)}")
cassette, chain 12 116 4 12 126 6 14 116 2 14 126 14 16 116 4 16 126 2 18 116 2 18 126 18 21 116 1 21 126 21 26 116 2 26 126 2 32 116 4 32 126 2 chainring, chain 30 116 2 30 126 6 39 116 1 39 126 3 50 116 2 50 126 2
Now imagine a cog is bent slightly on one of your cogwheels. Maybe because a small rock stuck there in chain for a moment. If cogwheel in cassette has 14 cogs and chain has 126 links, a cogwheel will rotate 126/14=9 times for a full rotation of chain. (GCD(14,126)=14.) This is bad. Because this faulty cog will touch each time every 9 links in chain, but not other. Of course, a faulty cog will gradually destroy these 9 links (out of 126). These worn links may become weak, leading to a sudden break.
What can you do? Of course, you want the links in your chain to wear in a balanced manner. This is possible for a pair with 21 cogs in cogwheel and 116 links in chain, because GCD(21,116)=1. That means that faulty cog will touch each link in chain (out of 116) and it will wear evenly -- and this is good. Metal weariness will be 'distributed' along all links.
The same can be generalized to a faulty link in chain (maybe with a small rock stuck in it) that touches all cogs in cogwheel (GCD=1) or only some of them (GCD!=1).
The same can be generalized to any mechanisms with cogwheels and chains.

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.